Equação - Na matemática, uma equação é uma igualdade envolvendo uma ou mais variáveis (valores desconhecidos).
São exemplos de equações as seguintes igualdades:
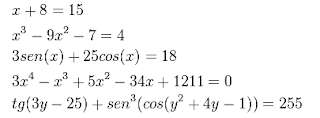
Equações do 1º Grau
Definição: Toda sentença matemática expressa por uma igualdade, na qual exista uma ou mais letras que representem números, é denominada equação. Cada letra que representa este número desconhecido é chamada de variável ou incógnita.
Numa equação existem dois membros e cada membro é constituído por termos.
Exemplo: Na equação, 3x +2 = 5 −x temos:
O símbolo = separa os membros ; Os símbolos =, + e – separam os termos.
1º membro: 3x + 2
2º membro: 5 − x
Incógnita: x
Termos: 3x , 2 , 5 e − x
Termos com incógnita: 3x e − x
Termos independentes: 2 e 5
Exercício 1. Considera a equação, x + 5 = 7 Indica:
1) a incógnita;
2) o 1º membro;
3) o 2º membro;
4) os termos independentes;
5) os termos com incógnita.
Exercício 2. Considera a equação, 2x + 5 = 7 − 3x + 2 Indica:
1) a incógnita;
2) o 1º membro;
3) o 2º membro;
4) os termos independentes;
5) os termos com incógnita.
Exercício 3. Considera a equação, 3x + 5 − x = 4x − 5 − x Indica:
1) a incógnita;
2) o 1º membro;
3) o 2º membro;
4) os termos independentes;
5) os termos com incógnita.
A importância do estudo das equações está no fato de que elas facilitam a resolução de certos problemas. Vejamos:
EXEMPLO 1
Dois pacotes juntos pesam 22 kg . Quanto pesa cada um deles, se o maior tem 6 kg a mais que o menor?
Já vimos que podemos representar quantidades desconhecidas usando a álgebra. Nesse caso, temos:
pacote menor = x
pacote maior = x + 6
Onde x representa o peso do pacote menor.
Então, teremos a seguinte equação: x + (x + 6) = 22
Efetuando as devidas equações:
x + (x + 6) = 22 Eliminar os parênteses
x + x + 6 = 22 Somar os termos semelhantes
2x + 6 = 22
2x + 6 - 6 = 22 - 6 Subtrair 6 nos dois membros
2x = 16
2x/2 = 16/2 Efetuar uma divisão por 2, nos dois membros
x = 8 Desse modo, o peso do pacote menor é de 8 kg e do pacote maior é de 8 + 6 = 14 kg .
EXEMPLO 2
Sabendo que o quádruplo de um número somado com 9 é igual ao número somado com 6, descubra qual é esse número.
Um número: x
Quádruplo do número: 4x
Equação correspondente: 4x + 9 = x + 6
Resolução:
4x + 9 = x + 6
4x - x = 6 - 9 passar + 9 para o segundo membro (fica-9) e + x para o primeiro membro (fica - x).
3x = - 3 como a operação inversa de :3 é x3,temos: x = - 3/3
x = - 1 Portanto, o número procurado é -1.
A verificação da solução
A verificação da solução é tão importante quanto a própria resolução da equação. Pois ela nos dá a possibilidade de descobrir se cometemos algum erro de cálculo, por exemplo, e corrigi-lo. Para fazer a verificação, basta experimentar o valor encontrado na incógnita. Veja:
4x + 9 = x + 6 substituindo x por - 1
4 (-1) + 9 = (- 1) + 6
- 4 + 9 = - 1 + 6
5 = 5
Logo, x = -1 é um valor que torna a equação 4x - 9 = x – 6 verdadeira.Experimente substituir x por qualquer outro valor, e veja o que acontece.
A raiz de uma equação
A solução de uma equação, isto é, o valor encontrado para a incógnita, é chamado, pela matemática, de raiz da equação.
x = - 1 é raiz da equação 4x + 9 = x + 6
EXEMPLO 3
Uma estante custa três vezes o preço de uma cadeira. Qual o preço da estante, se as duas mercadorias juntas custam R$ 64,00?
Equacionando o problema:
Preço da cadeira: x
Preço da estante: 3x
Equação correspondente: x + 3x = 64
Resolução:
x + 3x = 64
4x = 64 _ x = 64/4 = 16 _ x = 16
Verificação da raiz:
16 + 3 . 16 = 64
16 + 48 = 64
64 = 64
A estante custa R$ 48,00.
Exercícios
1) Resolva as equações:
a) 4x + 8 = 3x - 5
b) 3a - 4 = a + 1
c) 9y - 11 = - 2
d) 5x - 1 = 8x + 5
2) Verifique se - 7 é raiz da equação: 2(x + 4) – x/3 = x - 1
3) Invente um problema cuja solução pode ser encontrada através da equação: 2x - 3 = 16
4) Ana e Maria são irmãs e a soma de suas idades é igual a 35. Qual a idade de Ana, se Maria é 5 anos mais nova?
5 )Qual é o número que dividido por 5 é igual a 6?
6) Qual é o número que multiplicado por 7 é igual a 3?
7) Qual é o número que somado com 5 é igual a 11?
8) Qual é o número que somado com 6 é igual a - 13?
9) Uma indústria produziu este ano 600.000 unidades de um certo produto. Essa produção representou um aumento de 20%, em relação ao ano anterior. Qual a produção do ano anterior?
São exemplos de equações as seguintes igualdades:
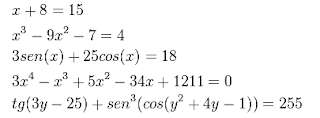
Equações do 1º Grau
Definição: Toda sentença matemática expressa por uma igualdade, na qual exista uma ou mais letras que representem números, é denominada equação. Cada letra que representa este número desconhecido é chamada de variável ou incógnita.
Numa equação existem dois membros e cada membro é constituído por termos.
Exemplo: Na equação, 3x +2 = 5 −x temos:
O símbolo = separa os membros ; Os símbolos =, + e – separam os termos.
1º membro: 3x + 2
2º membro: 5 − x
Incógnita: x
Termos: 3x , 2 , 5 e − x
Termos com incógnita: 3x e − x
Termos independentes: 2 e 5
Exercício 1. Considera a equação, x + 5 = 7 Indica:
1) a incógnita;
2) o 1º membro;
3) o 2º membro;
4) os termos independentes;
5) os termos com incógnita.
Exercício 2. Considera a equação, 2x + 5 = 7 − 3x + 2 Indica:
1) a incógnita;
2) o 1º membro;
3) o 2º membro;
4) os termos independentes;
5) os termos com incógnita.
Exercício 3. Considera a equação, 3x + 5 − x = 4x − 5 − x Indica:
1) a incógnita;
2) o 1º membro;
3) o 2º membro;
4) os termos independentes;
5) os termos com incógnita.
A importância do estudo das equações está no fato de que elas facilitam a resolução de certos problemas. Vejamos:
EXEMPLO 1
Dois pacotes juntos pesam 22 kg . Quanto pesa cada um deles, se o maior tem 6 kg a mais que o menor?
Já vimos que podemos representar quantidades desconhecidas usando a álgebra. Nesse caso, temos:
pacote menor = x
pacote maior = x + 6
Onde x representa o peso do pacote menor.
Então, teremos a seguinte equação: x + (x + 6) = 22
Efetuando as devidas equações:
x + (x + 6) = 22 Eliminar os parênteses
x + x + 6 = 22 Somar os termos semelhantes
2x + 6 = 22
2x + 6 - 6 = 22 - 6 Subtrair 6 nos dois membros
2x = 16
2x/2 = 16/2 Efetuar uma divisão por 2, nos dois membros
x = 8 Desse modo, o peso do pacote menor é de 8 kg e do pacote maior é de 8 + 6 = 14 kg .
EXEMPLO 2
Sabendo que o quádruplo de um número somado com 9 é igual ao número somado com 6, descubra qual é esse número.
Um número: x
Quádruplo do número: 4x
Equação correspondente: 4x + 9 = x + 6
Resolução:
4x + 9 = x + 6
4x - x = 6 - 9 passar + 9 para o segundo membro (fica-9) e + x para o primeiro membro (fica - x).
3x = - 3 como a operação inversa de :3 é x3,temos: x = - 3/3
x = - 1 Portanto, o número procurado é -1.
A verificação da solução
A verificação da solução é tão importante quanto a própria resolução da equação. Pois ela nos dá a possibilidade de descobrir se cometemos algum erro de cálculo, por exemplo, e corrigi-lo. Para fazer a verificação, basta experimentar o valor encontrado na incógnita. Veja:
4x + 9 = x + 6 substituindo x por - 1
4 (-1) + 9 = (- 1) + 6
- 4 + 9 = - 1 + 6
5 = 5
Logo, x = -1 é um valor que torna a equação 4x - 9 = x – 6 verdadeira.Experimente substituir x por qualquer outro valor, e veja o que acontece.
A raiz de uma equação
A solução de uma equação, isto é, o valor encontrado para a incógnita, é chamado, pela matemática, de raiz da equação.
x = - 1 é raiz da equação 4x + 9 = x + 6
EXEMPLO 3
Uma estante custa três vezes o preço de uma cadeira. Qual o preço da estante, se as duas mercadorias juntas custam R$ 64,00?
Equacionando o problema:
Preço da cadeira: x
Preço da estante: 3x
Equação correspondente: x + 3x = 64
Resolução:
x + 3x = 64
4x = 64 _ x = 64/4 = 16 _ x = 16
Verificação da raiz:
16 + 3 . 16 = 64
16 + 48 = 64
64 = 64
A estante custa R$ 48,00.
Exercícios
1) Resolva as equações:
a) 4x + 8 = 3x - 5
b) 3a - 4 = a + 1
c) 9y - 11 = - 2
d) 5x - 1 = 8x + 5
2) Verifique se - 7 é raiz da equação: 2(x + 4) – x/3 = x - 1
3) Invente um problema cuja solução pode ser encontrada através da equação: 2x - 3 = 16
4) Ana e Maria são irmãs e a soma de suas idades é igual a 35. Qual a idade de Ana, se Maria é 5 anos mais nova?
5 )Qual é o número que dividido por 5 é igual a 6?
6) Qual é o número que multiplicado por 7 é igual a 3?
7) Qual é o número que somado com 5 é igual a 11?
8) Qual é o número que somado com 6 é igual a - 13?
9) Uma indústria produziu este ano 600.000 unidades de um certo produto. Essa produção representou um aumento de 20%, em relação ao ano anterior. Qual a produção do ano anterior?

























